The waveform of the transmitted signal can be described mathematically as:
s(t) = A(t)· sin[2πf(t)·t + φ(t)]
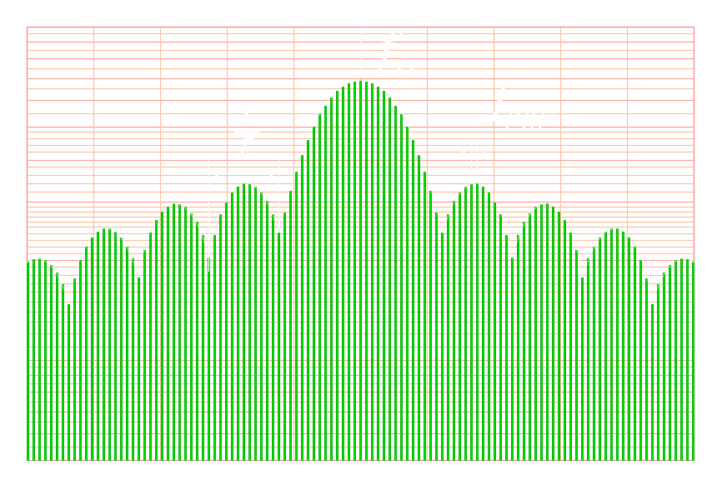
The function A(t) is a variation of the amplitude in the function of time t - ie an amplitude modulation. In the simplest case, the transmitter is for a short time switched on (for the time τ) and remains in the rest of the time in the “off position”. A(t) is then in the transmission case = 1, otherwise = 0. The function of time is then determined by the pulse repetition frequency and the duty cycle. Since the radar returns are subject to various losses, an actual amplitude modulation makes little sense except for just this switching function (On/off keying). The envelope of the frequency spectrum of a sequence of rectangular pulses is represented by a (sin x)/x function. The essential parts of the transmission power (note the logarithmic scale of the ordinate in the figure) are in a region BHF = 2/τ in the vicinity of the transmission frequency ftx.
The pulse repetition frequency fPRF and the duration of the transmitted pulse τ and the receiving time (Τ − τ) have an influence on the performance of the radar, e.g. the minimal measuring range (the transmit pulse must have completely exited the antenna) and the maximum unambiguous range (the echo signal must be received in the time before the next transmission pulse).
The duration of the transmit pulse τ substantially affects the range resolution ΔR of pulse radar. The range resolution is:
ΔR = 0.5·τ·c (2)
The shorter the transmission pulse, the closer one behind the other two reflectors may be positioned so as to be nevertheless detected as two reflectors and not as one large object. The transmitter bandwidth BHF of the pulse radar increases with decreasing pulse width:
BHF = τ−1 (3)
The shortening of the pulses limits the maximum range in the case of simple pulse modulation. Under these conditions, the pulse energy Ep can be increased only by the pulse power PS at a required range resolution.
For the maximum range of the pulse radar, the pulse energy is crucial, and not its pulse power:
Significant improvements in this situation can be achieved with the internal modulation of the transmit pulse (intra-pulse modulation). The relationship between the duration of the transmit pulse and the duration of the received pulse is resolved by the pulse compression in the receiver. A location of various reflectors and the measurement of its individual range can also be carried out within the duration of the transmit pulse.
The function φ(t) in equation (1) is the expression for a phase shift of the whole signal. The initial phase of the transmitted signal can either be known and can be predictable (due to the generation of oscillation). In this case, the pulse radar is attributable to the fully coherent radars. The actual phase angle can also be known but the initial state can be unpredictable. Then the radar is one of the pseudo-coherent radars. If this initial phase completely indeterminate (chaotic), then the radar is one of the non-coherent radars. Only with a possible phase-encoded Intra Pulse modulation, this function gets more importance.

Significant improvements in this situation can be achieved with the internal modulation of the transmit pulse (intra-pulse modulation). The relationship between the duration of the transmit pulse and the duration of the received pulse is resolved by the pulse compression in the receiver. A location of various reflectors and the measurement of its individual range can also be carried out within the duration of the transmit pulse.
The function φ(t) in equation (1) is the expression for a phase shift of the whole signal. The initial phase of the transmitted signal can either be known and can be predictable (due to the generation of oscillation). In this case, the pulse radar is attributable to the fully coherent radars. The actual phase angle can also be known but the initial state can be unpredictable. Then the radar is one of the pseudo-coherent radars. If this initial phase completely indeterminate (chaotic), then the radar is one of the non-coherent radars. Only with a possible phase-encoded Intra Pulse modulation, this function gets more importance.